En el artículo sobre nuevos sensores «Aptina» que he publicado esta mañana: Ftc 9-10-2012, Nicolas se hacía esta interesante pregunta:
1″ – área 13.54(H) x 9.22(V): Es el tamaño del sensor de la Nikon 1, pero nunca entenderé que parte del sensor mide 1″. Si alguien lo sabe se agradece la explicación.
Ostras Nicolas, es una pregunta que yo también me he hecho algunas veces, pero siempre la había dejado correr.
Hoy me ha picado la curiosidad y la elevo aquí a categoría de artículo para ver si alguien nos puede iluminar.
Para centrar ideas, os cuento:
- El sensor de la Nikon 1, que es de 1 pulgada, mide según las especificaciones: 13,2 x 8,8 mm. Eso da una diagonal de 15,8 mm.
- Un sensor FF mide 36 x 24 mm. Eso da una diagonal de 43,26 mm.
43,26 / 15,8 da exactamente 2,7, que es el factor de recorte aplicado al sistema Nikon 1. Por lo tanto no hay ningún error.
Que yo sepa, y creo que la crisis todavía no la ha encogido, una pulgada tiene 25,4 mm.
¿ Nos habremos inventado eso de que el sensor de la Nikon 1 mide 1 pulgada ?.
Pues no. El sensor de la Sony RX100 mide lo mismo, y también dice que es un sensor de 1 pulgada: ver especificaciones en «Dpreview»
Así que la pregunta sigue en vigor.
¿ Que parte del sensor de la Nikon 1 ó de la Sony RX100 es la que mide 1 pulgada ?
Como me ha picado todavía más la curiosidad he hecho los cálculos con otro tamaño de sensor.
Por ejemplo: la última Samsung EXF2 tiene un sensor de 1/1,7″, es decir de 14,94 mm.
Bien. Las dimensiones del sensor son de 7,44 x 5,58 mm, lo que da una diagonal de 9,30 mm, que tampoco coincide con los 14,94 que reza su apartado tamaño.
Y ahora lo que resulta más curioso:
En la Nikon 1: 25,4/15,8 da 1,6 ; pero en la Samsung EXF2: 14,94/9,3 también da 1,6, con lo cual no se trata de un error. Simplemente ya ves, Nicolas, nos estamos perdiendo algo.
¿ Alguien sabe que relación tiene supuesto tamaño de un sensor, con sus medidas, y con su diagonal ?.
Ostras. Solo se que no se nada. Y ante la duda ¡¡¡ Socorro !!!
Actualización: 10-10 – 2012
De entrada muchas gracias a todos por vuestras aportaciones. Ya veo que el tema no tiene solución, o al menos no tiene una solución seria y rigurosa.
A partir del artículo de «Dpreview» que nos ha facilitado «Peperplejo» en su comentario y que no conocía, veo que el presunto tamaño del sensor corresponde al diámetro de un circulo arbitrario de los antiguos «tubos vidicon» utilizados para las cámaras de TV a mitad del siglo pasado. Ese diámetro respecto al tamaño real del área de captación mantenía una relación totalmente arbitraria pues dependía de la «cantidad de vidrio» sobrante en la fabricación del susodicho tubo.
Lo único que se me ha ocurrido es comprobar, a partir de los datos que da «Dpreview», si existe una relación más o menos constante entre el diámetro arbitrario del circulo y la diagonal real del sensor.
Para ello os muestro aquí una tabla EXCEL que he elaborado a partir de la de «Dpreview». Simplemente le he añadido una columna final en la que se muestra la relación entre ambas cantidades. Veréis en el resultado que la relación no es constante, pero está acorada entre los valores de 1,4 y 1,6. Haciendo la media de las 13 relaciones sale 1,5.
Así pues, y siendo consciente de que este resultado es solo una aproximación y hasta que no tengamos una explicación o una solución mejor, yo propongo el valor de 1,5 como solución de compromiso:
Así pues, si tenemos las dimensiones del un sensor (ancho, alto y diagonal), podremos saber cual es su tamaño en la nomenclatura habitual de fracciones de pulgadas simplemente multiplicando su diagonal x 1,5 y después pasando esa cantidad a un quebrado o una fracción.
Por ejemplo:
- Un sensor que mida 6,4 x 4,8 mm, tiene una diagonal de 8 mm (lo dijo Pitágoras hace mucho tiempo).
- 8 mm x 1,5 = 12 mm
- 1 pulgada tiene 25,4 mm
Luego el tamaño del sensor sería 1/2,11″, lo que aproximaremos a 1/2″
O a la inversa, por ejemplo:
- Un sensor de 2/3″ tiene un diámetro de circulo arbitrario de 16,933 mm.
- 16,933 / 1,5 = 11,28 mm que sería la diagonal del sensor.
En realidad vemos en la tabla que es 11.00 mm, pero la aproximación es suficientemente buena como para hacer cálculos de factor de recorte y demás.
También podemos ver que en los sensores más grandes, que son los más habituales hoy en día, esa relación se aproxima más a 1,6 que a 1,5, y por tanto quizás fuera mejor tomar como factor de conversión un número más próximo a 1,6 que a 1,5, incluso el mismo 1,6.
Ya lo se. Soy consciente de que esto no es ninguna solución rigurosa, pero es que la definición del diámetro del circulo del sensor tampoco lo es, y por tanto no hay manera de sacar ninguna conclusión exacta.
Lo que no acabo de entender es por qué arrastramos estas reliquias del pasado que la verdad no hacen más que confundir. De los años 50 ya han pasado más de 60 años, y no creo que nadie se molestara si definiéramos los tamaños simplemente por la diagonal real del área de captación de un sensor expresada en milímetros ¿ no ?
Bueno. Mucha salud para todos y ojalá este tipo de problemas fueran los únicos a los que tuviéramos que enfrentarnos es estos turbulentos tiempos que nos ha tocado vivir.

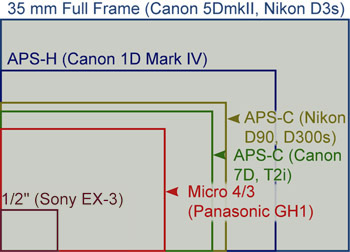

Es que resulta que es prácticamente imposible hallar una correlación matemática lógica…
Las nomenclaturas de fracciones en el sistema imperial (pulgadas) guardan relación al tamaño de los tubos Vidicon para las cámaras de video de los años 50 y viene a representar 2/3 del espacio aprovechable del diametro del tubo (ojo, encima es un valor aproximado)
Un galimatías basado en una tecnología obsoleta pero que sigue en uso en el mercado anglosajón. Son así de raros…
Aquí lo explican más o menos… http://www.dpreview.com/learn/?/key=sensor%20sizes
Al final es como el chiste, de por que la gente no sabe aparcar, pero en versión yankie. Ahora me pregunto si vivía mas feliz en la ignorancia. 😉
Perplejo, gracias por la aclaración.
Inspirándome en la solución de perplejo, he encontrado una relación matemática bastante curiosa.
Si dibujamos un circulo que abarque el sensor, la mitad de su perímetro es igual a la medida de la supuesta diagonal.
Sera coincidencia, pero con esta solución duermo mejor.
Ostras Nicolas. Supongo que en la busqueda de una solución coherente y en aras a poder dormir tranquilo, has enloquecido y has llegado a una solución en plan cachondo ¿no? ¿ O quizás es que no te he entendido bien ?.
Si trazamos un circulo que abarque al sensor resultará que el diámetro del circulo coincide necesariamente con la diagonal del sensor, y tu dices que la mitad del perímetro coincide con la diagonal. Eso no puede ser.
La longitud de la circunferencia es 2pr ó pd (donde «r» sería el radio o «d» el diametro, y «p» es el número «pi» – no he sabido escribir aquí su símbolo). Pero «d» también es la diagonal del cuadrilátero que define el sensor.
La mitad del perímetro del circulo, o sea de la longitud de su circunferencia es pr ó pd/2.
Entonces tu estás diciendo que pd/2 = d, lo cual evidentemente no puede ser cierto. ¿ no ?
He actualizado el artículo y he llegado a una solución de compromiso que al menos sirve para salir del paso, porque con rigurosidad matemática no hay ninguna solución. ¿ A ver que te parece ?
No se merecen Nicolás… Efectivamente el asunto es para mear y no echar gota :)…
No sois los primeros (ni los últimos) en estar haciendo cálculos de pulgadas a milímetros sin entender absolutamente nada… 🙂
Un saludo…
Adolfo:
Pongo un ejemplo, cojemos el senor de la Nicon 1. Dibujamos el circulo mas pequeño que abarque todo el sensor. Y el perímetro de ese circulo es 51,4mm que partido entre dos da 25,7 casi 1″
Dicho de otra manera: el «tamaño» de un sensor es igual a la longitud del arco que abarca su diagonal.
Pero al final los tres hacemos lo mismo:
perplejo 3/2 = 1,5
adolfo 1,5
nicolas pi/2 = 1,57
Ostras. El método cientifico ha sido aplicado. Tres geniales investigadores han llegado a la misma conclusión. El problema está resuelto y la solución es entre 1,5 y 1,6, pongamos 1,55.
Como decían los faraones en tiempos bíblicos: «Que asi se escriba, y así se cumpla».
Tema resuelto y asunto cerrado. A otra cosa.
Mucha salud y muchas gracias a todos.
Uffff…..que dolor de cabeza.
Que bueno adolfo XD.